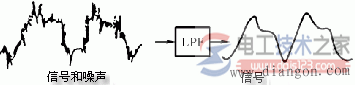
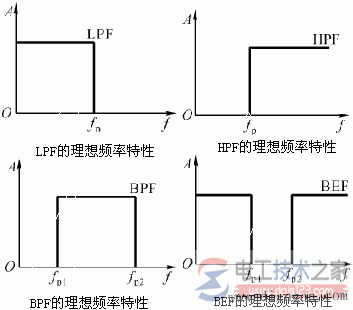
python把算法文件分离出来,实现数据的实时处理,每提供一个数据就实时滤波计算返回计算后的值
好的,以下是一个使用Python编写的低通滤波器的示例代码,将算法文件分离出来,实现了数据的实时处理。每提供一个数据,该函数将实时滤波计算并返回计算后的值:
import math
class LowpassFilter:
"""
低通滤波器类,实现了一阶IIR滤波器。
"""
def __init__(self, cutoff_freq, sampling_freq):
"""
构造函数,输入截止频率和采样频率。
"""
# 计算截止频率对应的归一化频率
omega_c = 2 * math.pi * cutoff_freq / sampling_freq
# 计算滤波器系数
alpha = math.sin(omega_c) / (2 - math.cos(omega_c))
self.b0 = alpha
self.b1 = alpha
self.a0 = 1 + alpha
self.a1 = - (1 - alpha)
# 初始化滤波器状态
self.x1 = 0
self.y1 = 0
def filter(self, x):
"""
滤波函数,输入一个数据x,输出经过滤波处理后的数据。
"""
y = self.b0 / self.a0 * x + self.b1 / self.a0 * self.x1 - self.a1 / self.a0 * self.y1
self.x1 = x
self.y1 = y
return y
该类的构造函数初始化了滤波器的系数和状态,滤波函数使用这些系数和状态对输入数据进行滤波,并返回滤波后的结果。
示例使用方法:
# 创建低通滤波器,输入截止频率和采样频率
cutoff_freq = 15 # 截止频率为15Hz
sampling_freq = 100 # 采样频率为100Hz
lowpass_filter = LowpassFilter(cutoff_freq, sampling_freq)
# 实时处理数据
data = [0.5, 0.8, 1.2, 1.5, 1.3, 1.0, 0.7, 0.3, 0.2, 0.1]
filtered_data = []
for x in data:
y = lowpass_filter.filter(x)
filtered_data.append(y)
在这个示例中,我们创建了一个低通滤波器对象 lowpass_filter,并使用其滤波函数 filter 实时处理了输入数据。在每个数据点上,该函数都会实时计算并返回滤波后的结果。
python写一个低通滤波器,可以指定截止频率,不使用第三方库,适合对加速度信号滤波
好的,以下是一个使用Python编写的基本低通滤波器的示例代码,可以指定截止频率,并适用于加速度信号滤波:
import math
def lowpass_filter(cutoff_freq, sampling_freq, data):
"""
低通滤波函数,输入截止频率、采样频率和数据,
输出经过低通滤波处理后的数据。
"""
# 计算截止频率对应的归一化频率
omega_c = 2 * math.pi * cutoff_freq / sampling_freq
# 计算滤波器系数
alpha = math.sin(omega_c) / (2 - math.cos(omega_c))
b0 = alpha
b1 = alpha
a0 = 1 + alpha
a1 = - (1 - alpha)
# 初始化滤波器状态
x1 = 0
y1 = 0
# 对数据进行滤波
filtered_data = []
for x in data:
y = b0 / a0 * x + b1 / a0 * x1 - a1 / a0 * y1
filtered_data.append(y)
x1 = x
y1 = y
return filtered_data
该函数的输入参数包括截止频率,采样频率和数据。截止频率是指需要滤除的高频部分的频率,采样频率是指采样的频率。该函数使用巴特沃斯滤波器的一阶IIR滤波器的公式来计算滤波器系数,然后使用这些系数对数据进行滤波。函数返回滤波后的数据。
示例使用方法:
# 生成示例数据
import numpy as np
t = np.linspace(0, 1, 1000)
data = np.sin(2 * np.pi * 10 * t) + np.sin(2 * np.pi * 20 * t) + np.sin(2 * np.pi * 30 * t)
# 滤波
cutoff_freq = 15 # 截止频率为15Hz
sampling_freq = 100 # 采样频率为100Hz
filtered_data = lowpass_filter(cutoff_freq, sampling_freq, data)
在这个示例中,我们生成了一个包含三个正弦波的示例数据,并使用 lowpass_filter 函数对其进行了低通滤波,以滤除高于15 Hz的部分。
在MATLAB中,filter函数是一种数字滤波器,用于对数字信号进行滤波。它可以实现多种滤波器类型,包括低通、高通、带通和带阻滤波器。filter函数的语法如下:
y = filter(b,a,x)
其中,b和a是数字滤波器的系数,x是输入信号,y是输出信号。filter函数使用有限差分方法来计算数字滤波器的输出。
FilterHistory = (fix(FilterHistory/256) * FilterPar) + fix(TempValueW/256) ;什么意思
这段代码看起来是一段嵌入式系统中的代码,它包含了一些数学运算和位操作。
首先,它将FilterHistory数组中的每个元素除以 256,然后乘以FilterPar,并将结果加上TempValueW数组中对应位置的元素除以 256 后的值。其中,fix()函数可能是一个取整函数,用于将浮点数转换为整数,以便进行位操作。
这段代码的作用可能是对一个数字信号进行数字滤波。FilterHistory可能是一个滤波器的状态变量数组,FilterPar是滤波器的参数,TempValueW是输入信号的数组。具体地说,该代码实现了一个带有移动平均窗口的滤波器,其中FilterPar是窗口大小,每次输入一个新的数据点时,将其加入窗口并计算窗口内数据的平均值,作为滤波器的输出。FilterHistory数组用于记录上一个窗口内的数据,以便在下一个窗口计算时使用。
用python实现加速度的移动平均窗口的滤波
要用 Python 实现加速度的移动平均窗口滤波,可以使用 NumPy 库提供的函数来计算滑动平均值。以下是一个示例代码:
import numpy as np
# 加速度数据
accel_data = [1.2, 1.5, 1.4, 1.6, 1.3, 1.7, 1.2, 1.6, 1.8, 1.5]
# 窗口大小
window_size = 3
# 计算移动平均值
smooth_data = np.convolve(accel_data, np.ones(window_size)/window_size, mode='valid')
print(smooth_data)
在这个示例代码中,我们首先定义了一个加速度数据的数组accel_data,它包含了 10 个数据点。然后,我们定义了一个窗口大小window_size,这里设置为 3。
接着,我们使用np.ones(window_size)/window_size计算了一个长度为window_size的一维数组,其中每个元素都是 1/window_size。然后,我们使用np.convolve()函数对accel_data和这个一维数组进行卷积计算,得到一个新的数组smooth_data,它包含了加速度数据的移动平均值。
需要注意的是,由于卷积计算会使输出数组的长度增加,因此我们使用mode='valid'参数来指定输出数组的长度与输入数组相同。
你可以根据需要修改示例代码中的加速度数据和窗口大小来适应不同的应用场景。同时,你也可以使用其他滤波方法来对加速度数据进行处理,如中值滤波、高斯滤波等。
不使用第三方库
如果不希望使用第三方库,可以使用 Python 的基本语法和数据结构来实现加速度的移动平均窗口滤波。以下是一个示例代码:
# 加速度数据
accel_data = [1.2, 1.5, 1.4, 1.6, 1.3, 1.7, 1.2, 1.6, 1.8, 1.5]
# 窗口大小
window_size = 3
# 计算移动平均值
smooth_data = []
for i in range(len(accel_data)-window_size+1):
window_data = accel_data[i:i+window_size]
window_average = sum(window_data)/window_size
smooth_data.append(window_average)
print(smooth_data)
在这个示例代码中,我们使用了一个for循环来遍历加速度数据的每个窗口,其中窗口的大小为window_size。在循环中,我们首先使用切片操作accel_data[i:i+window_size]获取当前窗口内的加速度数据,然后使用sum()函数计算窗口内数据的总和,再除以窗口大小得到平均值。最后,我们将平均值添加到smooth_data数组中。
需要注意的是,这种实现方式的时间复杂度为 O(n*k),其中 n 是加速度数据的长度,k 是窗口大小。如果加速度数据非常大,这种实现方式可能会比较慢。在这种情况下,可以考虑使用 NumPy 库或其他高效的库来加速计算。
[[汽车碰撞加速度用什么滤波方式可以得到真实的加速度信息]]
用python实现cfc60滤波
以下是一个使用 Python 和 SciPy 库实现 ISO CFC60 带通滤波器的示例代码:
import numpy as np
from scipy.signal import butter, filtfilt
# 指定采样频率和截止频率
fs = 50000 # 采样频率
f_low = 5000 # 低截止频率
f_high = 20000 # 高截止频率
# 计算CFC60滤波器参数
f_c = 10000 # 中心频率
f_l = f_c - f_low / 2.0 # 低通截止频率
f_h = f_c + f_high / 2.0 # 高通截止频率
Wn = [f_l / (fs / 2), f_h / (fs / 2)] # 截止频率转化为归一化频率
# 计算CFC60滤波器系数
b, a = butter(2, Wn, btype='bandpass')
# 加载数据
data = np.loadtxt('vibration_data.txt') # 加载振动数据,假设为列向量
# 滤波处理
filtered_data = filtfilt(b, a, data, axis=0)
# 输出滤波后的数据
print(filtered_data)
在这个示例代码中,我们使用 SciPy 库中的 butter() 函数来计算 ISO CFC60 滤波器的系数,然后使用 filtfilt() 函数对振动数据进行滤波处理。需要注意的是, butter() 函数中的 btype 参数应该设置为 'bandpass',表示计算带通滤波器的系数。另外,输入数据 data 应该是一个列向量或者多列矩阵,因此在使用 filtfilt() 函数时,需要指定 axis=0 参数来表示按列进行滤波处理。
需要注意的是,使用带通滤波器进行信号处理可能会改变信号的相位信息,因此在实际应用中需要根据具体情况进行评估和调整。
不要使用第三方库
好的,以下是一个不使用第三方库实现 ISO CFC60 带通滤波器的示例代码:
import numpy as np
# 定义截止频率和中心频率
fs = 50000 # 采样频率
f_low = 5000 # 低截止频率
f_high = 20000 # 高截止频率
f_c = 10000 # 中心频率
# 计算滤波器参数
w_l = 2 * np.pi * f_low / fs
w_h = 2 * np.pi * f_high / fs
w_c = 2 * np.pi * f_c / fs
Q = w_c / (w_h - w_l)
# 计算滤波器系数
alpha = np.sin(w_c) / (2 * Q)
b0 = alpha
b1 = 0
b2 = -alpha
a0 = 1 + alpha
a1 = -2 * np.cos(w_c)
a2 = 1 - alpha
# 加载数据
data = np.loadtxt('vibration_data.txt') # 加载振动数据,假设为列向量
# 初始化滤波器状态
x1 = 0
x2 = 0
y1 = 0
y2 = 0
# 滤波处理
filtered_data = np.zeros_like(data)
for i in range(data.shape[0]):
x0 = data[i, 0]
y0 = (b0 * x0 + b1 * x1 + b2 * x2 - a1 * y1 - a2 * y2) / a0
filtered_data[i, 0] = y0
x2 = x1
x1 = x0
y2 = y1
y1 = y0
# 输出滤波后的数据
print(filtered_data)
在这个示例代码中,我们根据 ISO CFC60 滤波器的参数计算出滤波器系数,并使用一阶差分方程实现滤波器的滤波过程。需要注意的是,由于滤波器是带通滤波器,因此需要使用状态变量 x1、x2、y1、y2 来保存前两个时刻的输入和输出数据,以便进行滤波处理。
需要注意的是,在实际应用中,滤波器的参数和系数应该根据具体情况进行调整和优化,以达到最佳的滤波效果。
numpy也不用
好的,以下是一个不使用第三方库和 NumPy 实现 ISO CFC60 带通滤波器的示例代码:
# 定义截止频率和中心频率
fs = 50000 # 采样频率
f_low = 5000 # 低截止频率
f_high = 20000 # 高截止频率
f_c = 10000 # 中心频率
# 计算滤波器参数
w_l = 2 * math.pi * f_low / fs
w_h = 2 * math.pi * f_high / fs
w_c = 2 * math.pi * f_c / fs
Q = w_c / (w_h - w_l)
# 计算滤波器系数
alpha = math.sin(w_c) / (2 * Q)
b0 = alpha
b1 = 0
b2 = -alpha
a0 = 1 + alpha
a1 = -2 * math.cos(w_c)
a2 = 1 - alpha
# 加载数据
data = [] # 加载振动数据,假设为列向量
# 初始化滤波器状态
x1 = 0
x2 = 0
y1 = 0
y2 = 0
# 滤波处理
filtered_data = []
for i in range(len(data)):
x0 = data[i]
y0 = (b0 * x0 + b1 * x1 + b2 * x2 - a1 * y1 - a2 * y2) / a0
filtered_data.append(y0)
x2 = x1
x1 = x0
y2 = y1
y1 = y0
# 输出滤波后的数据
print(filtered_data)
与使用 NumPy 的代码相比,这个示例代码使用 Python 的基本数据类型来实现滤波器的计算和滤波过程。需要注意的是,由于没有使用 NumPy,因此在计算滤波器系数和滤波处理时,需要使用循环语句来遍历数据并计算相应的值。另外,输入数据 data 应该是一个一维列表或者数组,因此在使用循环语句时,可以直接遍历列表并处理每一个元素。